Polinomios

¡Bienvenid@ a Polinomios.org!

Somos una web especializada en los polinomios, así que aquí encontrarás toda la teoría sobre los polinomios y, además, podrás practicar con ejercicios resueltos paso a paso de cada tema. Hemos explicado cada tema al detalle para que se entienda todo bien y de manera fácil, ¡pero si te queda alguna duda no dudes en escribirla en los comentarios! Te contestaremos rápidamente. 😉 Solo tenemos un objetivo: ¡que consigas la mejor nota de la clase! 😍

¿Qué es un polinomio?

La definición de polinomio es la siguiente:

En matemáticas, un polinomio es una expresión algebraica formada por números, letras y exponentes. Es decir, un polinomio consiste en la suma o resta de diferentes términos o monomios. Los números de un polinomio se llaman coeficientes y las letras de un polinomio son sus variables.

Por lo tanto, para poder entender el significado de un polinomio primero debes saber qué son los monomios. Te dejamos esta página donde se explica detalladamente por si aún no lo tienes del todo claro. Además, allí podrás ver todos los tipos de monomios y cómo se hacen las operaciones con monomios, entre otras cosas.

Por ejemplo, la siguiente expresión se trata de un polinomio de segundo grado:

Como puedes ver, este polinomio de grado 2 está formado por 3 monomios distintos que se suman o se restan.

¿Cuáles son las partes de un polinomio?

Una vez sabemos en qué consiste un polinomio, vamos a ver cuáles son y cómo identificar las partes de un polinomio:

• Términos: cada monomio que forma parte del polinomio.
• Coeficientes: los números que acompañan a cada término del polinomio.
• Grado: el mayor exponente al que está elevada la variable del polinomio.
• Variable: es la letra que tiene el polinomio.
• Término principal: es el término de mayor grado de polinomio.
• Término independiente: aquel término del polinomio que no posee variable.
• Coeficiente principal: coeficiente del término principal del polinomio.

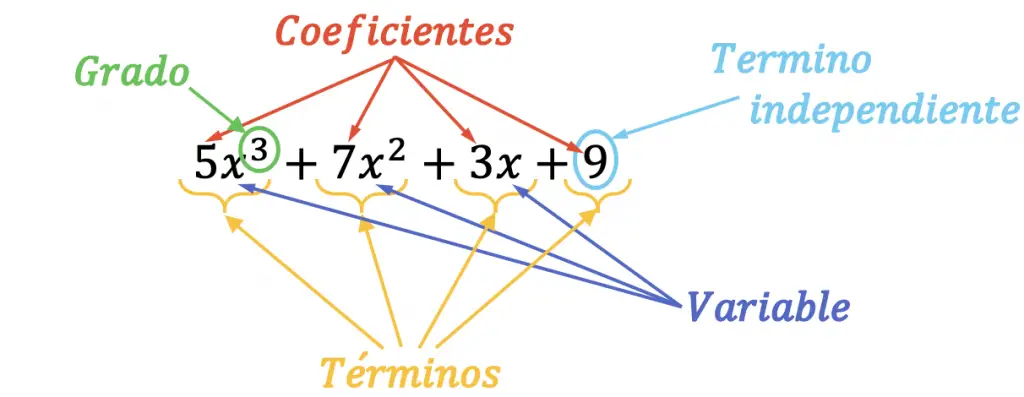
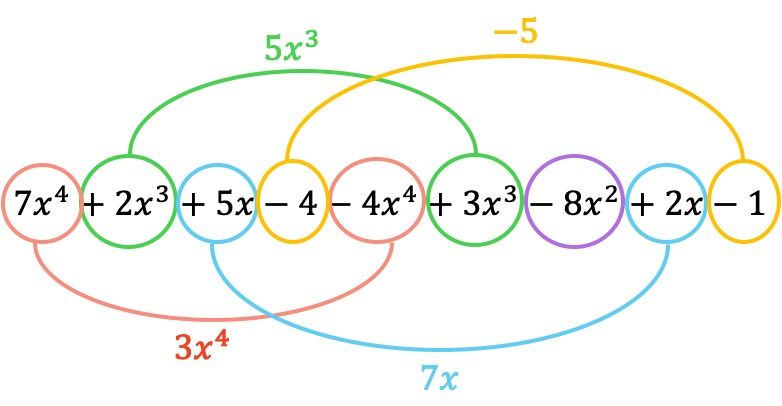
En el polinomio anterior de tercer grado puedes ver todas sus partes o elementos señalizados. Además, el término principal de dicho polinomio es 5x³, porque es el monomio de mayor grado. Asimismo, el coeficiente principal del polinomio es 5, ya que es el coeficiente del término principal.

Ejemplos de polinomios

Para acabar de entender el concepto de polinomio, a continuación vamos a ver varios ejemplos de polinomios:

• Polinomio de grado cero:

Aunque parezca extraño, una constante sola también puede ser un polinomio. Se trata de un polinomio de un único término.

• Polinomio de primer grado:

• Polinomio de segundo grado:

• Polinomio de tercer grado:

• Polinomio de cuarto grado:

Tipos de polinomios

Los polinomios pueden clasificarse según los siguientes tipos:

• Polinomio ordenado: es aquel polinomio que tiene todos sus términos ordenados de mayor a menor grado.

  

• Polinomio completo: es aquel polinomio que tiene todos sus términos desde el monomio de mayor grado hasta el término independiente.

  

• Polinomio incompleto: es aquel polinomio que le falta como mínimo un término de algún grado.

  

• Polinomio homogéneo: es aquel polinomio el cual todos sus términos son del mismo grado.

  

• Polinomio heterogéneo: es aquel polinomio en el que no todos sus términos tienen el mismo grado.

  

• Polinomio opuesto: un polinomio es opuesto a otro si los coeficientes de los términos de igual grado son del mismo valor pero de signo contrario.

  

  

• Polinomio mónico: es aquel polinomio que tiene una única variable y cuyo coeficiente principal es igual a 1.

  

• Polinomio multivariable: es aquel polinomio que posee más de una variable.

  

Por otro lado, debes saber que existen dos clases de polinomios muy importantes, ya que se suelen hacer muchas operaciones con ellos: los binomios y los trinomios. Te dejamos los siguientes enlaces donde explicamos detalladamente qué es un binomio y qué es un trinomio. Además, en estas páginas encontrarás qué hace tan especial a cada uno de estos dos tipos de polinomios y para qué se utilizan.

Operaciones con polinomios

Con los polinomios se pueden hacer todo tipo de operaciones: sumar, restar, multiplicar, dividir, potencias,… A continuación vamos a ver cómo se hace cada una de estas operaciones polinómicas.

Suma de polinomios

Para resolver la suma de dos o más polinomios se deben sumar los términos de los polinomios que son semejantes. Es decir, la suma de polinomios consiste en sumar los términos que tienen la misma parte literal (mismas variables y mismos exponentes).

Así pues, existen dos métodos para sumar polinomios:

• Suma de polinomios vertical: primero se colocan los dos polinomios sumandos uno debajo del otro, de manera que los términos semejantes de los dos polinomios estén alineados por columnas. Y luego se suman los coeficientes de cada columna manteniendo las partes literales de los monomios intactas:

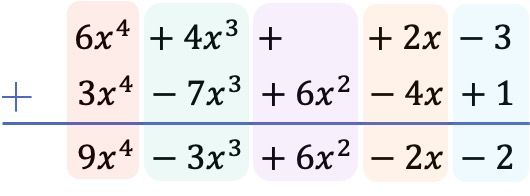
• Suma de polinomios horizontal: en este caso no hace falta poner los polinomios ordenados, sino que se suman directamente los términos que tienen partes literales idénticas, o dicho con otras palabras, los términos con las mismas variables (letras) y los mismos exponentes. Los términos que no son semejantes no se pueden sumar.

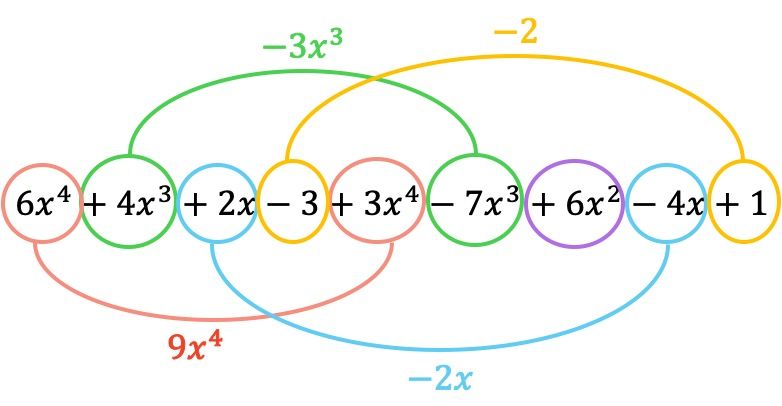
Ahora que ya sabes cómo se suman los polinomios, te recomendamos que practiques haciendo ejercicios resueltos de suma de polinomios.

Resta de polinomios

Para hacer la resta de dos polinomios se deben restar los términos de los polinomios que son semejantes. Es decir, la resta de polinomios se basa en restar los términos que tienen la misma parte literal (mismas variables y mismos exponentes).

Al igual que con la suma de polinomios, la resta de polinomios se puede realizar verticalmente y horizontalmente:

• Resta de polinomios vertical:
  1. Primero de todo, se ponen los polinomios ordenados uno debajo del otro.
  2. En segundo lugar, se cambia de signo a todos los términos del polinomio sustraendo.
  3. Finalmente, se suman los coeficientes de los monomios con el mismo grado.

1

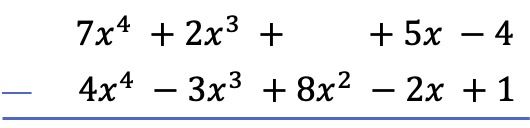
2

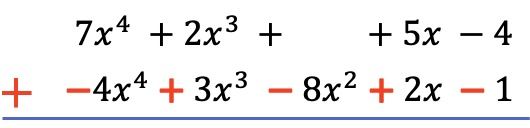
3

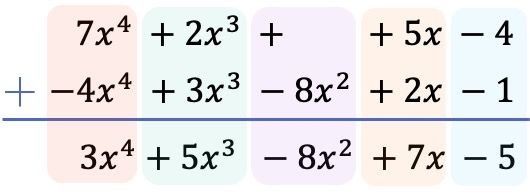
• Resta de polinomios horizontal:
  1. En primer lugar, se colocan los 2 polinomios con paréntesis uno detrás del otro.
  2. Luego se cambia el signo de todos los monomios que forman parte del polinomio que resta, ya que tiene un signo negativo delante.
  3. Por último, se agrupan los términos cuya parte literal es igual.

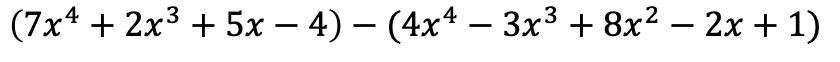
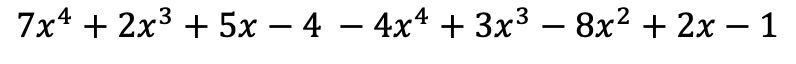
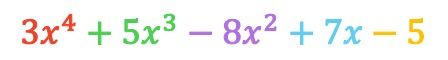
Es bastante común equivocarse resolviendo una resta de polinomios, así que te recomendamos que practiques haciendo estos ejercicios resueltos de resta de polinomios.

Multiplicación de polinomios

Fíjate cómo se multiplican dos polinomios con el siguiente ejemplo:

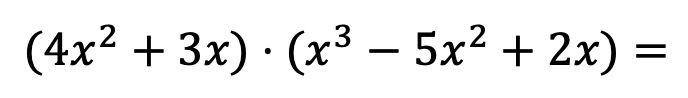
En primer lugar, tenemos que multiplicar cada elemento del primer polinomio multiplicador por cada término del segundo polinomio:

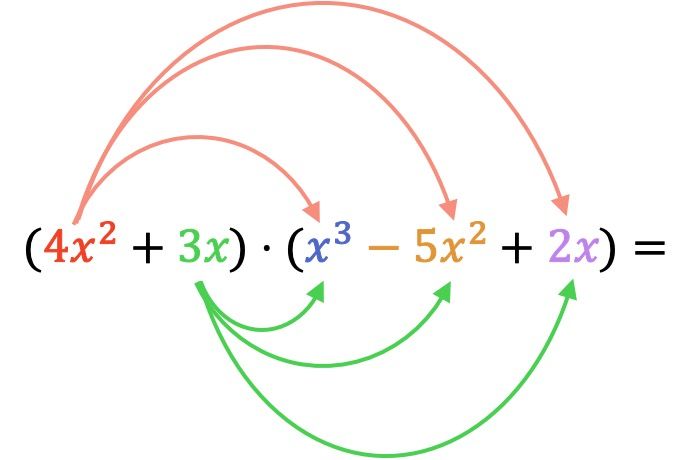
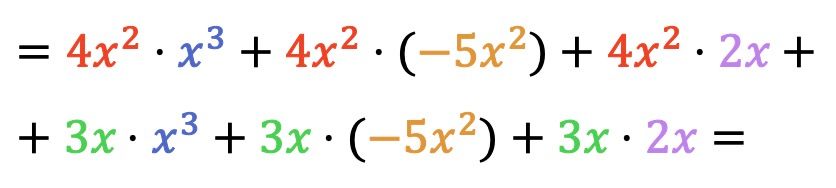
Ahora hacemos todas las multiplicaciones de monomios:

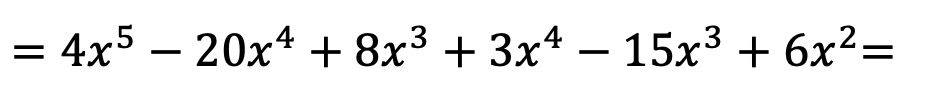
Una vez hemos multiplicado los dos polinomios entre sí, tan solo tenemos que agrupar los términos resultantes que sean semejantes:

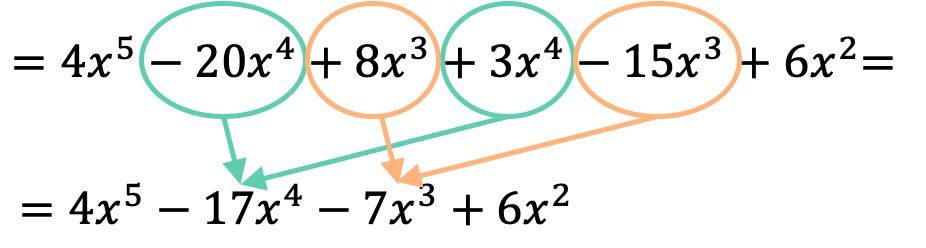
De modo que el resultado de la multiplicación polinómica es:

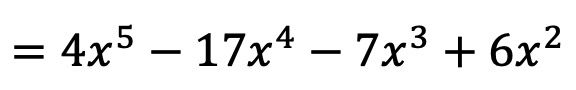
Acabamos de ver cómo se multiplican dos polinomios entre sí, pero debes saber que el procedimiento es un poco diferente cuando multiplicamos un polinomio por número o un monomio. En el siguiente enlace podrás ver cómo se hacen todos estos tipos de productos entre polinomios y, además, podrás practicar con ejercicios resueltos de multiplicación de polinomios.

División de polinomios

Para dividir dos polinomios se debe de seguir un procedimiento complicado, así que vamos a ver cómo se dividen dos polinomios resolviendo un ejemplo paso a paso:

Lo primero que debemos hacer es colocar los polinomios en forma de división. A la izquierda escribimos el numerador de la fracción (polinomio dividendo) y a la derecha ponemos el denominador de la fracción (polinomio divisor):

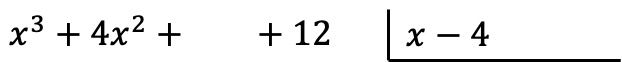
Atención: Si un un polinomio no tiene un monomio de un determinado grado, tenemos que dejar un hueco en su lugar. Por ejemplo, el polinomio no tiene término de grado 1, por eso hay un espacio en blanco en su lugar.

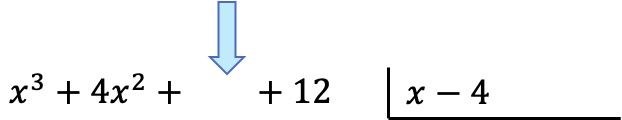
Una vez hemos puesto los polinomios en su sitio, vamos a hallar el cociente. Y para encontrar el primer término del cociente tenemos que dividir el primer término del dividendo entre el primer término del divisor:

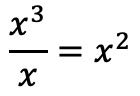
Y ponemos el resultado de la división en el lugar del cociente:

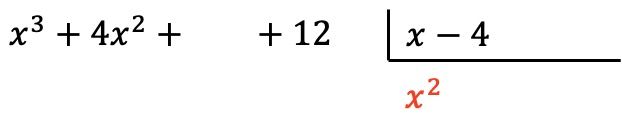
Ahora multiplicamos el término encontrado por cada elemento del divisor, y cada resultado lo ponemos debajo del dividendo en su columna correspondiente cambiándole de signo:

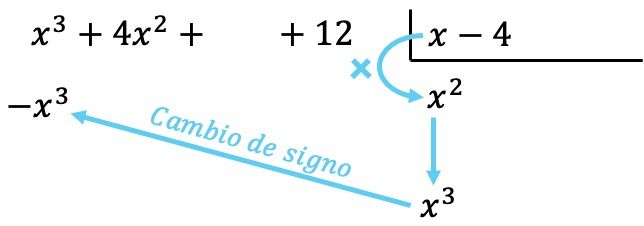
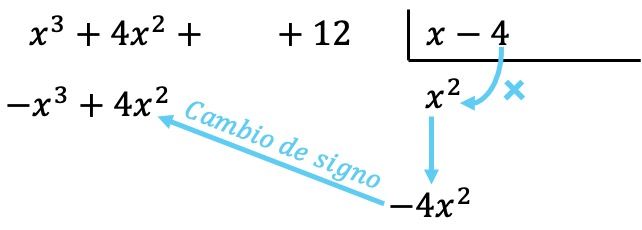
Como sucede en todas las operaciones con polinomios, es importante ordenar los polinomios de mayor a menor grado de manera que todos los términos de un mismo grado estén situados en una misma columna.

Una vez hemos colocado los resultados de las multiplicaciones con el signo contrario, debemos sumar los términos que están alineados verticalmente:

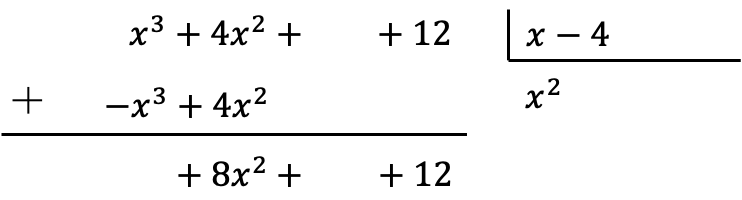
Fíjate que al hacer esta suma el coeficiente de mayor grado se anula y, por tanto, tenemos un término menos en el dividendo.

Ahora tenemos que ir repitiendo el mismo procedimiento hasta que el polinomio dividendo sea de menor grado que el polinomio divisor.

De modo que volvemos a dividir el primer término del dividendo entre el primer término del divisor:

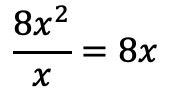
Colocamos el resultado en el cociente:

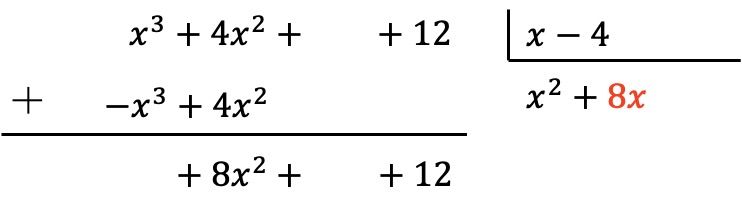
Igual que antes, multiplicamos el nuevo término del cociente por cada elemento del divisor y ponemos los resultados con el signo contrario en las columnas correspondientes del dividendo:

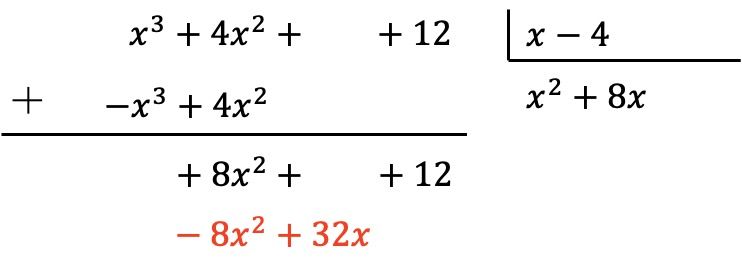
Y sumamos verticalmente:

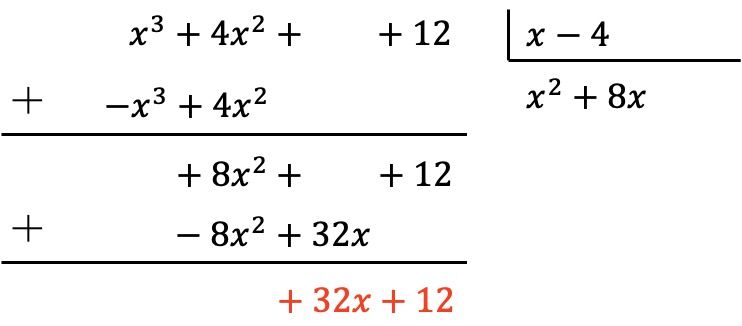
El polinomio dividendo aún no es de menor grado que el polinomio divisor, por lo que debemos seguir haciendo el mismo proceso.

Así que primero dividimos el primer término del dividendo entre el primer término del divisor, en segundo lugar multiplicamos el resultado por cada término del divisor, luego ponemos los resultados cambiados de signo en el dividendo y, finalmente, sumamos verticalmente:

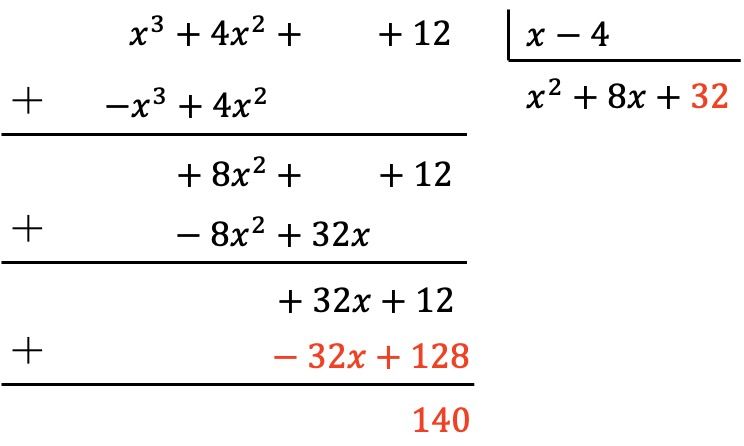
De manera que ya hemos conseguido que el polinomio dividendo sea de grado inferior que el grado del divisor, porque el dividendo es de grado 0 y el divisor de grado 1. En consecuencia, la división queda terminada.

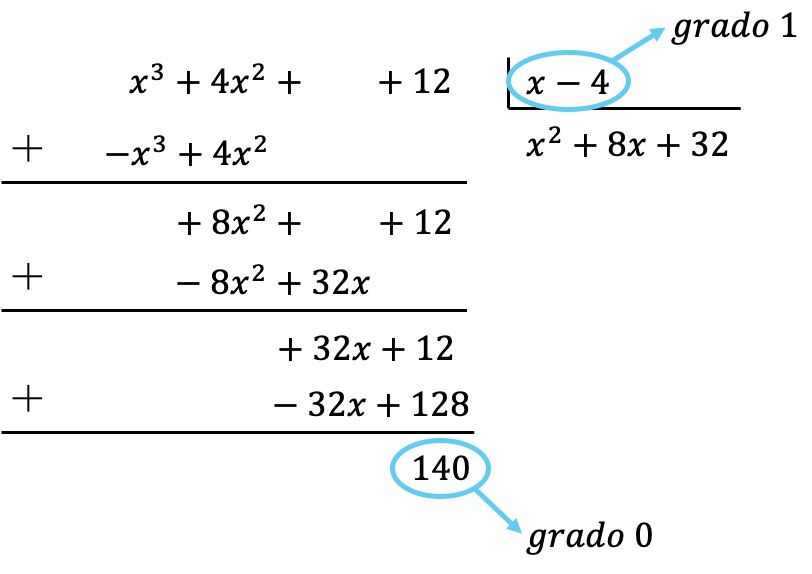
Así que el resultado de la división polinomial es:

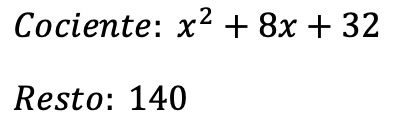
Como has podido comprobar, la división de polinomios es un procedimiento complejo, por eso te recomendamos que practiques e intentes hacer estos ejercicios resueltos de división de polinomios. En este enlace no solo hallarás ejercicios resueltos de diferente dificultad, sino que, además, podrás ver cuáles son las propiedades de esta operación y cómo se divide un polinomio entre un monomio (procedimiento distinto).

Por otro lado, también debes saber que existe un método que sirve para dividir algunos polinomios muy concretos. Y la gran ventaja de este método es que es mucho más rápido y mucho más fácil de hacer que el procedimiento que acabamos de ver, por lo que merece la pena saber en qué consiste y cuándo se puede usar este método, llamado la regla de Ruffini. Haz click en este enlace y descubre cómo se dividen dos polinomios de manera fácil.

Identidades notables

Las identidades notables, también conocidas como productos notables o igualdades notables, son reglas matemáticas que permiten resolver de manera directa algunas operaciones con polinomios.

Las identidades notables más comunes son el cuadrado de una suma, el cuadrado de una diferencia (o resta), y la suma por la diferencia.

Descubre cómo se aplican estas fórmulas en ejercicios resueltos de las identidades notables. Además, en este enlace podrás ver todas las identidades notables, ya que aquí solo te hemos podido enseñar 3 pero en realidad hay muchísimas más.

Sacar (o extraer) factor común de un polinomio

Cuando dos o más términos de un polinomio tienen un factor común, se puede sacar (o extraer) factor común para transformar las sumas o restas del polinomio en una multiplicación.

Puede que escrito te parezca un poco difícil, así que mejor veamos cómo se extrae factor común de un polinomio mediante un ejemplo:

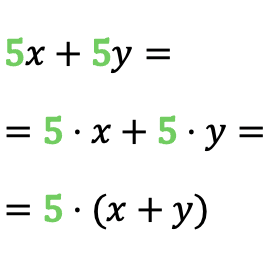
Como puedes ver en el ejemplo, el número 5 está repetido en el monomio 5x y en el monomio 5y, por lo tanto, el factor común del polinomio es 5. Entonces, una vez hemos identificado el factor común, podemos convertir la suma de monomios en un producto.

Esta operación es bastante complicada y, de hecho, se suelen cometer muchos errores sacando factor común. Por eso te recomendamos que practiques haciendo ejercicios resueltos de sacar factor común. En la página enlazada no solo podrás hacer ejercicios, sino que también te enseñamos a cómo sacar factor común en fracciones y, además, cómo sacar factor común por el método de agrupación.

Factorización de un polinomio

La factorización de polinomios es una técnica que se utiliza en matemáticas para descomponer un polinomio en el producto de factores.

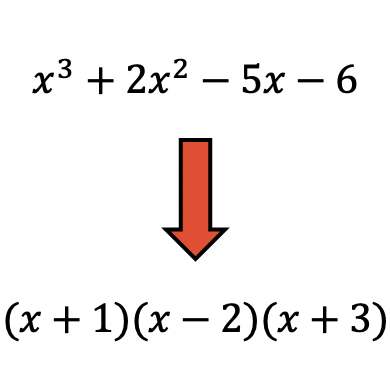
La factorización de polinomios resulta muy útil ya que es más fácil hacer operaciones con polinomios factorizados.

Sin embargo, para explicar este procedimiento se necesita una página entera. Por eso hemos hecho una guía donde explicamos paso a paso cómo factorizar polinomios, allí te mostramos todos los métodos que existen para factorizar un polinomio de manera que tú puedas escoger el que prefieras. Además, te enseñamos algunos casos especiales de la factorización de polinomios. Y, finalmente, también podrás practicar con ejercicios resueltos.

Valor numérico de un polinomio

El valor numérico de un polinomio P(x) para el valor x=a, es decir P(a), es el resultado que se obtiene al sustituir la variable x del polinomio por el número a y hacer los cálculos indicados en la expresión del polinomio.

Por ejemplo, el valor numérico del polinomio para se calcula de la siguiente manera:

Historia de los polinomios

Las expresiones algebraicas, como por ejemplo los polinomios, se usan en los problemas más antiguos de la matemática. Sin embargo, el álgebra que entendemos y utilizamos nosotros hoy en día se empezó a desarrollar en el siglo XV. A continuación, haremos un repaso de la evolución histórica de los polinomios.

Ya en las civilizaciones antiguas de Egipto y Babilonia se planteaban resolver ecuaciones de primer o de segundo grado y relaciones del estilo a² + b² = c² mediante las propiedades de los polinomios. Más tarde, alrededor del año 300 a.C., Euclides desarrolló un método que permitía resolver algunos de estos tipos de ecuaciones desde un enfoque geométrico.

Más tarde, en la época medieval, los islámicos consiguieron generalizar algunas ecuaciones en forma de binomios, y ya se usaba la letra X como variable de los polinomios. Así pues, en esa época ya se sabía cómo resolver polinomios lineales y cuadráticos, pero los polinomios de tercer grado siempre han resultado ser más difíciles históricamente. Fue el matemático italiano Leonardo de Pisa, también conocido como Fibonacci, quien en el siglo XIII logró hacer una primera aproximación de los polinomios cúbicos (x³ + 2x² + cx = d). Y, finalmente, durante el principio del siglo XVI, los matemáticos italianos Tartaglia, Scipone del Ferro y Gerolamo Cardano descifraron un método que servía para hallar las raíces de este tipo de polinomios. 

Cabe destacar que este fue un gran paso no solo en la evolución de los polinomios, sino de las matemáticas en general, ya que a partir de este avance surgirían los números complejos más adelante. Pero este tema ya lo discutiremos en otro artículo porque da para mucho debate.

Siguiendo con la historia de los polinomios, en el siglo XVI los científicos Tartaglia y Cardano fueron también los responsables de descubrir una fórmula que permitía solucionar polinomios de cuarto grado. Por contra, los polinomios de quinto grado aún se resistían y no se les encontraba ninguna solución. De hecho, en 1824, el noruego Niels Henrik Abel logró demostrar que no puede existir ninguna fórmula para polinomios de grado 5 o superior, resulta matemáticamente imposible.

Por oro lado, antes de esta demostración, durante el siglo XVII René Descartes publicó su famosa obra ‘La Géométrie’. En ella explicó la relación entre la geometría y el álgebra y, en nuestro caso lo más importante, introdujo la gráfica de una ecuación polinómica. Es decir, logró deducir cómo representar una función polinómica en un gráfico. Aunque esto quizás ahora puede parecer como algo muy simple de realizar, en aquella época resultó ser un gran avance.

Actualmente, los polinomios se utilizan en la gran mayoría de problemas matemáticos. Por eso los polinomios ya se empiezan a enseñar en los institutos en los cursos de 1º ESO y 2º ESO y se profundiza en el concepto resolviendo tantos ejercicios en 3º ESO y 4º ESO, e, incluso, en Bachillerato.